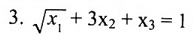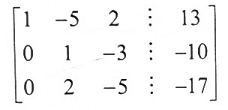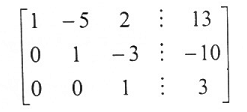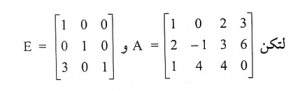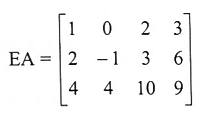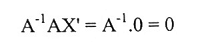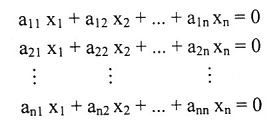نظام المعادلات الخطية، المعادلات تم تأسيسها على يد محمد الخوارزمي في كتابة الجبر والمقابلة، يعتبر محمد الخوارزمي مؤسس الجبر أحد فروع الرياضيات .
محتويات
تعريف المعادلات
المعادلة هي التساوي بين عبارتين وتكون هذه المعادلة إما صحيحة لقيم معينة للمجهول وخاطئة لقيم أخرى.
مثال :-
2x+1=7 تكون المعادلة صحيحة عندما تكون x=3 وتكون المعادلة خاطئة لأي قيمة أخرى. فنقول أن هو حل المعادلة لأنه عند التعويض بقيمة x تساوي 3 تصبح المعادلة 2(3)+1=7 وهذا صحيح وأصبح الطرفان متساويان.
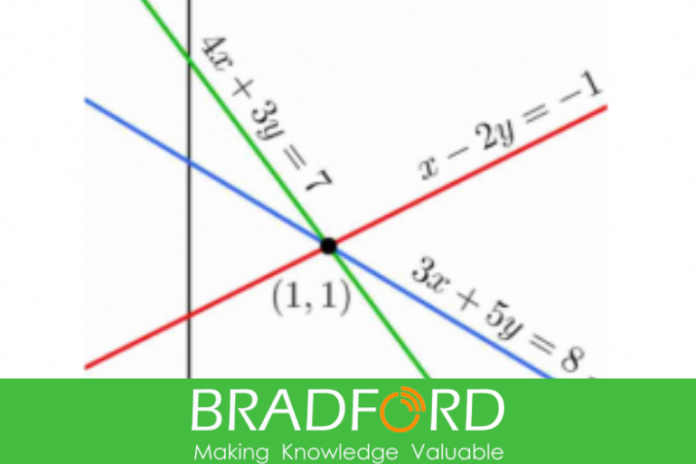
يمكن تمثيل معادلة الخط المستقيم في المستوى x-y بالصيغة:
ax + by = c
يتم تمثيل هذه الصيغة بمعادلة خطية من المتغيرين x و y ويمكن كتابة المعادلات الخطية التي تحتوي على n من المتغيرات وتكتب كالتالي
a1x1 + a2x2 + …. + anxn = c
حيث c، an، … ، a2، a1 ثوابت حقيقة . وحل هذه المعادلة هي الأعداد sn ، … ، s2، s1 بحيث يتم تحقيق المعادلة عندما نعوض xn = sn، … ، x2 = s2 ، x1 = s1
مثال ( 1 )
نظام المعادلات الخطية
1.x + 2y = 8
2.x1 – 2x2 + 4x3 + x4 = 7
3.y = x +3/4 z
المعادلات الغير خطية
1.x + 2y2 =3
2.y – cos θ = 0
نلاحظ أن صيغة المعادلة الخطية تحتوي على متغيرات من الدرجة الأولى ولا تحتوي تلك المعادلات الخطية على متغيرات بدرجة أعلى، جذور، دوال مثلثية، ضرب متغيرات مع بعضها البعض أو دوال أسية.
يوجد أنظمة خطية تحتوي على معادلتين بثلاث متغيرات :
مثال ( 2 ) :
3x1 = x2 + 5x3 = – 4
4x1 – x2 – 3x3 = 1
وتكون قيم هذه المتغيرات : x1 = 1 ، x2 = 2 ، x3 = -1
هي حل النظام وذلك لأنها تحقق كل من المعادلتين ولكن x1 = 1 و x2 = 8 و x3 = 1 ليسو حلا لأنها لا تحقق كل من المعادلتين.
يوجد بعض الأنظمة ليس لها حل ومثال على ذلك
X + y = 6
2x + 2y = 10
والسبب لعدم إيجاد حل هو عند ضرب المعادلة الثانية في 1/2 نحصل على هذا النظام
X + y = 6
X + y = 5
وبالتالي يتناقضان مع بعضهما البعض.
يتم تسمية النظام الخطي الذي يوجد له حل واحد فقط بالنظام المستقل والنظام الذي ليس له حل يسمى بالنظام الغير مستقل.
المعنى الهندسي للنظام الخطي
يتم تمثيل النظام الخطي الذي يتكون من معادلتين خطيتين بمتغيرين هما x و y كالتالي
a1x +b1y = c1
A2x + b2y = c2
ويكون الشكل الهندسي لهذه المعادلات هو الخط المستقيم L1 و L2 كل خط مستقيم على حدى أما إذا كانت النقطة (x,y) تقع على المستقيم إذا كانت x و y تحقق معادلة المستقيم فتصبح حلول النظام الخطي هو تقابل المستقيمين.
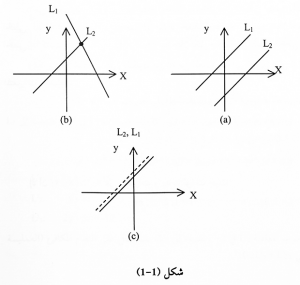
يوجد ثلاث احتمالات للحلول وهي :-
- المستقيمان المتوازيان ، لا يوجد نقطة تقاطع وبالتالي ليس للنظام الخطي حل كما في الرسمة a.
- المستقيمان يتقاطعان بنقطة ، ذلك يعني أن النظام الخطي له حل واحد فقط كما في الشكل b.
- المستقيمان متطابقان وبالتالي يوجد عدد غير محدود من الحلول كما في الشكل c.
نظام المعادلات الخطية
ما نستنتجه من ذلك أن النظام الخطي أما ليس له أي حلول أو له حل واحد فقط أو له عدد لا نهائي من الحلول.
المجموعة المنتهية التي تتكون من m من المعادلات الخطية تحتوي على n المتغيرات xn،…،، x2 ، x1 نظام المعادلات الخطية. وكذلك تسمى بالنظام الخطي. إما المتتابعة التي تتكون من n من الأعداد الحقيقية sn، … ، s2، s1 = xn حل لكل معادلة من النظام الخطي.
يمكن كتابة النظام الخطي الذي يتكون من m من المعادلات التي تحتوي على n من المتغيرات كالتالي
a11x1 + a12x2 + … + a1m xn = c1
X21x1 + a22x2 + … + a2m xn = c2
… … …
am1 +am2 x2 + … + amn xn = cm
فإن المتغيرات xn ، … ، x2 ، x1 هي متغيرات وثوابت حيث أن 1،2،…..،m i=، j=1،2،….n
قد يفيدك : اهم مواد تخصص الهندسة الكهربائية
طريقة حل أنظمة المعادلات الخطية
يتم حل نظام المعادلات الخطية عن طريق إستبدال نظام معطى بنظام جديد يوجد به مجموعة الحل نفسها ولكن يكون أسهل في الحل. يوجد بعض الخطوات للحصول على هذا النظام الجديد عن طريق تطبيق ثلاث أنواع من العمليات وذلك لحذف المجاهيل:
- تبادل معادلتين لبعضهما.
- ضرب معادلة بثابت غير صفري.
- جمع مضاعف إحدى المعادلات الى أخرى.
مثال ( 3 ) :
نظام المعادلات الخطية
الحل:
1- نضرب المعادلة L1 في 3- ونضيف حاصل ضرب للمعادلة L2.
يرمز لهذه المعادلة بالرمز L2 + -3L1، ونضرب L1 في 4- ونضيفه إلى L3 أي أن العملية هي L3 + -4L1
من خلال هاتين العمليتين نحصل على النظام المكافئ كالتالي
نظام المعادلات الخطية
2- ضرب المعادلة L2 في 2- ونضيفه إلى L’2 وهكذا سنحصل على النظام المكافئ وتصبح العملية هي L’23 + -2L’2
نظام المعادلات الخطية
من L”3 نحصل على z = 3 وبتعويضها في L”2 نحصل على y = -1 وأخيرا نعوض عن z،y في L”1 فنحصل على x = 2 أي أن مجموعة الحل هي (3 ، -1 ، 2)، نلاحظ أن النظام الخطي 3 يكافئ النظام 1. ويسمى النظام 3 نظام خطي تبعا للصيغة المدرجة خطيا.
مثال ( 4 ) :
الحل:
بإستخدام نفس طريقة حل المثال السابق
يتبين من المعادلتين أننا حصلنا على معادلتين خطيتين بثلاث متغيرات ومن أجل الحصول على الحل نفرض أن z = t ثم نجد قيم y ، x وبالتعويض في المعادلة الثانية والأولي يكون الحل :-
Z = t ، y = 2+2t ، x = 2 – t
نلاحظ أن t في المثال تسمى بالوسيط وتكون الحلول في هذه الحالة غير منتهية وذلك لأنها تعتمد على t حيث أن t عدد حقيقي.
نلاحظ أيضا أنه اذا كان cn، …. ، c2،c1 في النظام الخطي 1 تساوي أصفار فإن هذا النظام يسمى بالنظام المتجانس، واذا كانت الثوابت cn، … ، c2، c1 لا تساوي أصفار فإن هذا النظام الخطي يسمى بالنظام الغير متجانس.
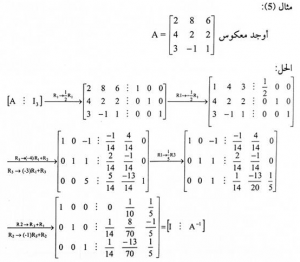
مثال ( 5 ) :
نظام المعادلات الخطية
الحل:-
عند تحويل هذا النظام إلى الشكل المدرج بإستخدام طريقة المثال رقم 2 نحصل على النظام المكافئ التالي:-
X + w = 0
Y + 7w = 0
Z + 6w = 0
نفرض أن t=w ونعوض بها في المعادلات، نحصل على:-
W = t ، Z = -6t ، y = -7t ، X = 11t
المصفوفة الممتدة : يمكن وضع الثوابت في النظام الخطي (1) بالصيغة :
إن aij هي أعداد حقيقية تمثل معاملات المتغيرات و ci تمثل الثوابت في الطرف الأيمن من النظام (1). تسمى الخطوط الأفقية صفوفاً، أما الخطوط العمودية فتسمى أعمدة، ويقال لهذه الصيغة ، المصفوفة الممتدة.
مثال ( 6 )
يوجد إمكانية وضع ثوابت النظام الخطي الواردة في 2 بصيغة مصفوفة ممتدة بهذا الشكل
الصفوف المتواجدة في المصفوفة الممتدة تقابل المعادلات الواردة في النظام الخطي للمثال 3 لذلك التعليمات الثلاثة المستخدمة في طريقة حل المعادلات الخطية تكافئ العمليات المستخدمة على صفوف المصفوفة الممتدة الآتية:
- يتم ضرب أي صف بكمية ثابتة ولكن غير صفرية
- تبديل أي صفين بوضع أحدهما مكان الآخر
- إضافة مضاعف أحد الصفوف لصف آخر
هذه العمليات تسمى بعمليات الصف البسيطة
مثال ( 7 )
حل النظام الخطي الوارد في المثال 3 عن طريق عمليات الصف البسيطة
الحل
1- المصفوفة الممتدة للنظام هي
2- نضرب الصف الأول في 3- ويتم إضافته إلى الصف الثاني ونضرب الصف الأول في 4- ويتم اضافته للصف الأول وبالتالي نحصل علي هذه المصفوفة الممتدة المكافئة :
3- نضرب الصف الثاني في 2- ويتم إضافتة إلى الصف الثالث:
هذه الصيغة تسمى الصيغة المدرجة التي تقابل النظام الخطي المكافئ:
عند التعويض عن z نحصل على
Z=3 ، y=1 ، x=2
المصفوفات البسيطة
المصفوفة البسيطة A هي المصفوفة المربعة اذا أمكن إيجادها من المصفوفة المحايدة In وذلك عن طريق إستخدام عملية صف بسيطة واحدة:
مثال ( 1 )
عند ضرب المصفوفة A بمصفوفة أولية مثل E من جهة اليسار، يكون تأثير ذلك معادلة لإجراء عملية صفية على A.
مثال ( 2 )
هذه مصفوفة بسيطة تم الحصول عليها من ضرب الصف الأول في 3 وإضافة حاصل الضرب إلى الصف الثالث من المصفوفة I3 .
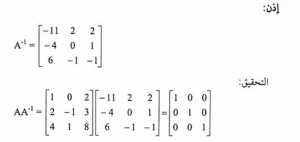
إذن :
يعادل هذا الشكل المصفوفة الناتجة من إضافة 3 أضعاف الصف الأول في A للصف الثالث فيها .
ملحوظة
اذا أثرت عملية صف بسيطة E على المصفوفة المحايدة In وذلك للحصول على مصفوفة بسيطة. فتوجد عملية صف ثانية إذا أثرت على E ستعيدها إلى In.
مثال ( 3 )
بفرض E مصفوفة تنتج من ضرب الصف رقم i في المصفوفة In بالثابت غير الصفري k.
عند ضرب الصف رقم i من المصفوفة E بالثابت 1/k ، نحصل على المصفوفة In ، هذه العمليات التي تعيد E إلى In تسمى العمليات العكسية.
قاعدة ( 2-1 )
كل مصفوفة بسيطة قابلة للإنعكاس وكذلك المعكوس مصفوفة بسيطة.
البرهان
بفرض أن مصفوفة بسيطة تنتج من تأثير عملية صفية بسيطة على In ، بفرض أن ‘E مصفوفة تنتج من تأثير معكوس هذه العملية على In ، وبإتباع تلك الملاحظة وحقيقة أن عمليات الصف العكسية تزيل تأثير أحدهما للأخرى فإن:
وهكذا فإن المصفوفة البسيطة E’ هي معكوس E.
قاعدة ( 3-1 )
بفرض أن A مصفوفة سعتها n x n فتكون الصيغ الآتية متكافئة ، وتكون إما جميعها صحيحة او جميعها خاطئة.
- A قابلة للإنعكاس.
- AX = 0 لها حل وحيد وهذا الحل هو الحل الصفري.
- الصيغة المدرجة الصفية المختزلة للمصفوفة A هي المصفوفة In.
- يعبر عن A كحاصل ضرب مصفوفات بسيطة.
البرهان
1←2 : بفرض أن A قابلة للإنعكاس وأن ‘X هو الحل لهذا النظام المتجانس AX = 0. لذا فإن AX’ = 0. لذا فإن AX’= 0.
A تكون قابلة للإنعكاس فإن A-1، تكون معكوس A، بضرب AX’ = 0بالمصفوفة A-1 من جهة اليسار نحصل على :
نظام المعادلات الخطية
وبالتالي تكون X’ = 0. نستنتج من ذلك أن الحل الوحيد هو الحل الصفري.
2←3 : بفرض أن AX = 0 هو الشكل المصفوفي للنظام الخطي:
نظام المعادلات الخطية
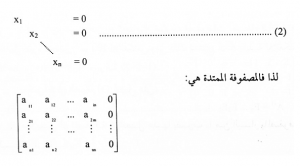
وبفرض أن حل هذا النظام هو الحل الصفري. فعند إستخدام طريقة إختزال جاوس ــ جوردان فإن المعادلات المقابله للشكل المدرج الصفي المختزل للمصفوفة الممتدة ستكون:
نظام المعادلات الخطية
وعند تطبيق عمليات الصف البسيطة على المصفوفة الممتدة للمعادلات الخطية (1) في هذه الحالة نحصل على المصفوفة الممتدة:
نظام المعادلات الخطية
وهذا يعني أن الصيغة المدرجة الصفية المختزلة للمصفوفة A هي In.
3←4 : وعند فرض أن الصيغة المدرجة الصفية المختزلة للمصفوفة A هو In.
يتم ضرب A من جهة اليسار بسلسلة من عمليات الصف البسيطة فتتحول A إلى In.
3) …………………………………E1E2…EnA=In
ولما كانت E1 ، E2 ، ….. ، En قابلة للإنعكاس، وبضرب طرفي المعادلة (3) بالمصفوفات نحصل على:
وتباعا إلى القاعدة (1-5-2) فإن A يتم التعبير عنها كحاصل ضرب مصفوفات بسيطة.
4←1 : إذا عبرنا عن A كحاصل ضرب مصفوفات بسيطة، فتكون A هي حاصل ضرب مصفوفات قابلة للإنعكاس ومن ذلك نستنتج أن A قابلة للإنعكاس [لاحظ قاعدة (1-4-5) وقاعدة (1-5-2)].
عند عكس طرفي الصيغة (3) نحصل على:
هذا يبين أن المصفوفة A يتم الحصول عليها من ضرب In من اليسار بالمصفوفات البسيطة En،….،E2،E1
وبمقارنة العلاقتين (3) و (5) يتضح أن سلسلة عمليات الصف التي تحول A إلى In ستحول In إلى A-1.
طريقة إيجاد معكوس المصفوفة القابلة للإنعكاس
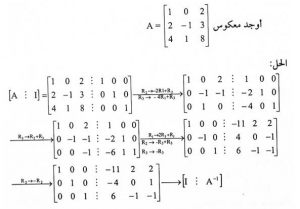
تحدث هذه الطريقة عن طريق إيجاد عمليات صف بسيطة تحول A إلى In ومن ثم يتم إستخدام نفس هذه السلسة من العمليات على المصفوفة المحايدة بجوار A للحصول على A-1.
لعمل ذلك يتم وضع المصفوفة المحايدة على يمين المصفوفة A للحصول على الشكل [A : In]. وبعد ذلك يتم إجراء عمليات الصف على هذه المصفوفة حتى يتم تحويل الجانب الأيسر الى In . وسيتم تحويل الجانب الأيمن الى A-1 عن طريق هذه العمليات ، وسنحصل على [In : A-1].
مثال ( 4 )
ملحوظة
لا يمكن معرفة إذا كانت A مصفوفة قابلة للإنعكاس أم لا. عندما تكون A غير قابلة للإنعكاس لايمكن اختزالها وتباعا الى العمليات الصفية البسيطة، أو بمفهوم آخر أن الشكل المدرج الصفي المختزل للمصفوفة A يحتوي على الأقل على صف واحد وتكون جميع عناصره أصفار.
مثال ( 6 )
الحل
بإتباع هذه الطريقة الموضحة في المثالين 4 و 5 يتم الحصول على:
نظام المعادلات الخطية
لا يفوتك : شاهد أفضل 11 كورس مجاني في مختلف المجالات
وهكذا فإن الصف رقم 3 من المصفوفة من الجهة اليسرى تكون جميع عناصره أصفار. وبالتالي تكون المصفوفة غير قابلة للإنعكاس.
يمكنكم التعرف بالتفاصيل على دوراتنا التدريبية ومحتوى كل كورس ومدته والأسعار والعروض الخاصة وتخفيضات الأسعار على هذا الرابط دورات تدريبية
إلى هنا انتهى مقالنا عن نظام المعادلات الخطية نرجو أن نكون قد قدمنا كل ما يفيدكم في مجال تعلمها والإستفادة منها ، ونرجو أن لا تبخلوا علينا بتعليق يضيف للمقال ويفيد باقي القراء.